基本信息

  • 标题: Scaling Large Language Model-Based Multi-Agent Collaboration
  • 作者: Chen Qian*, Zihao Xie*, YiFei Wang* 等（Zhiyuan Liu 与 Maosong Sun 为通讯作者）
  • 作者单位: Tsinghua University (清华大学), Peng Cheng Laboratory
  • 期刊/会议: ICLR 2025
  • 发表年份: 2025.03.17
  • DOI: 2406.07155
  • 开源地址: Github
  • 关键词: Multi-Agent Collaboration, Scaling Law, MACNET, Directed Acyclic Graphs

研究问题 (Research Questions)

受到“神经缩放定律（Neural Scaling Law）”的启发，探究在推理阶段不断增加智能体（Agent）的数量，是否也能像增加神经元那样，带来性能的持续提升？

研究背景 (Background)

神经缩放定律出自OpenAI 2020年发表的一篇论文《Scaling Laws for Neural Language Models》，提出了一个规律：随着模型变大、数据更多、算力更强，模型的Loss会按照幂律下降。而现在单个模型在进行封闭式推理时有局限性，特别是面对那些超出其文本训练边界的复杂情况时 。而且，它们往往是“快思考”（直觉反应），缺乏深度反思。多智能体协作被证明通常优于单个智能体，通过让智能体在互动环境中进行多轮对话，实际上是迫使它们进行“慢思考” (Slow Thinking)，也就是不断地反思和修正。虽然大家都知道多智能体好，但目前的绝大多数研究，智能体数量都非常少（通常少于10个，极少数能达到几十个）。

核心贡献 (Key Contributions)

  • 提出了MACNET框架(Multi-Agent Collaboration Network)，一个基于有向无环图 (DAG) 的多智能体协作框架，专门用于组织和编排大量的智能体进行任务求解。它将智能体分为两类：节点上的 Actor (执行者) 负责生成内容，边上的 Critic (批评者) 负责提供修改建议，通过这种分工实现高效协作。
  • 发现了“协作缩放定律” (Collaborative Scaling Law)，类似于神经网络的缩放定律，作者发现随着智能体数量的增加，任务完成质量呈现Logistic增长（S形曲线）。这证明了在推理阶段增加智能体数量（Scale up）是提升性能的一条有效路径，而且这种“协作涌现”比传统的神经元涌现发生得更早（不需要达到亿级参数那种规模）。
  • 论文对比了链式、树状、网状等多种结构，发现 不规则的拓扑结构（如随机连接） 往往比规则结构（如全连接网状）效果更好。这是因为随机连接能像“小世界网络”一样，在保持高效沟通的同时，避免信息过载。
  • 为了防止 1000 个智能体聊天导致上下文过长，作者设计了一种记忆控制机制：智能体之间只传递最终的“产物 (Artifact)”，而不传递之前的对话历史。这使得上下文长度的增长从平方级 $O(n^2)$ 降低到了线性级 $O(n)$，从而真正实现了大规模扩展。

MULTI-AGENT COLLABORATION NETWORK（MACNET）

Network Construction

作者借鉴了图的概念，使用了有向无环图的定义

$$\mathcal{G}=(\mathcal{V},\mathcal{E})$$ $$\mathcal{V}=\{v_{i}|i\in I\}$$ $$\mathcal{E}=\{\langle v_{i},v_{j}\rangle|i,j\in I\wedge i\ne j\}$$

其中$\mathcal{V}$ 表示由索引集 $I$ 索引的节点集合，$\mathcal{E}$ 表示边的集合，每条边都从一个节点指向另一个节点，且不存在环。图将负责编排智能体之间的交互，这类似于社交网络，信息通过有向边进行传播。直观地说，这种无环（Acyclic）特性防止了信息回流，消除了对特定任务进行“破环（cycle-breaking）”等额外设计的需求，从而增强了跨场景的通用性和适应性

由于穷举所有可能的拓扑结构是不切实际的，作者主要专注于三种主要类型——链式（chain）、树状（tree）和图状（graph），并进一步将其细分为如下图所示的六种代表性子拓扑。

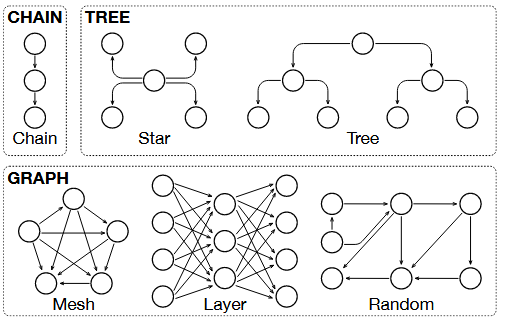
Figure 2

  • 链式拓扑：类似于瀑布模型，沿线性结构组织智能体之间的交互。
  • 树状拓扑：允许智能体进行分支，在独立的方向上进行交互；可进一步细分为“更宽”的星形（star-shaped）拓扑和“更深”的树形（tree-shaped）拓扑。
  • 图状拓扑：支持任意的交互依赖关系，节点拥有多个子节点和父节点，形成发散或收敛的交互；进一步归类为全连接网状（mesh）拓扑、MLP 状的分层（layered）拓扑以及不规则的随机（random）拓扑。

鉴于功能性二分（functional bipartition）——由发布指导性指令的监督型批评者（Critics）和提供定制产物的顺从型行动者（Actors）组成——能够有效地建立分工、激活功能性行为并促进循序渐进的任务解决 ，如下图所示，作者策略性地将一个批评者分配给每一条边，将一个行动者分配给每一个节点：

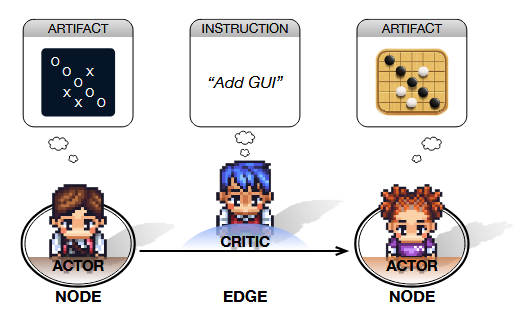
Figure 3

$$a_{i}=\rho(v_{i}), \forall v_{i}\in\mathcal{V}$$ $$a_{ij} = \rho(\langle v_{i},v_{j}\rangle), \forall\langle v_{i},v_{j}\rangle\in\mathcal{E}$$

其中 $\rho(x)$ 表示对元素 $x$ 进行的智能体化（agentization）操作，这是通过为基础模型配备上下文感知记忆、外部工具和专业角色来实现的；$a_{i}$ 和 $a_{ij}$ 分别表示分配给节点 $v_{i}$ 的行动者和分配给边 $v_{ij}$ 的批评者。

Interactive Reasoning

在过程式任务求解中，静态网络内智能体之间的交互推理需要策略性的遍历，以建立一个有序的交互标。在过程式任务求解中，静态网络内智能体之间的交互推理需要策略性的遍历，以建立一个有序的交互标准。在有向无环（DAG）的设定下，作者的图遍历策略遵循拓扑排序的原则，这确保了每个节点只有在其所有前置依赖都被遍历之后才会被访问。形式上，对于一个网络 $\mathcal{G}$，其拓扑顺序是智能体 $a_{i}$ 和 $a_{ij}$ 的一种线性排列，使得对于每一条有向边 $\langle v_{i},v_{j}\rangle\in\mathcal{E}$，该排列满足：

$$\forall\langle v_{i},v_{j}\rangle\in\mathcal{E},\mathbb{I}(a_{i})<\mathbb{I}(a_{ij})<\mathbb{I}(a_{j})$$

其中 $\mathbb{I}(x)$ 表示智能体 $x$ 在拓扑序列中的索引。这种排列确保了每个占据节点的智能体 $a_{i}$ 先于其对应的占据边的智能体 $a_{ij}$，而 $a_{ij}$ 又先于 $a_{j}$，从而确保信息沿着网络有序传播。

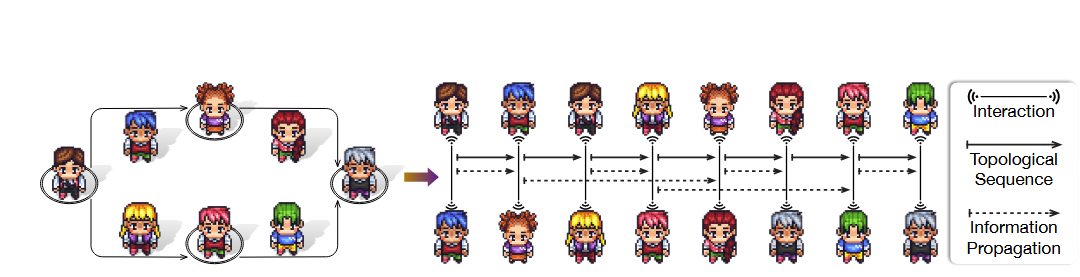
在建立全局顺序之后，如下图所示，作者启用每一对通过边连接的相邻智能体进行交互以实现产物精炼，这导致总共分配了 $|\mathcal{V}| + |\mathcal{E}|$ 个智能体，并至少需要 $2 \times |\mathcal{E}|$ 个交互轮次。具体而言，在每一条边内部，批评者（Critic）和行动者（Actor）之间的交互遵循一种双智能体多轮模式：

$$\tau(a_{i},a_{ij},a_{j}) = (\tau(a_{i},a_{ij}), \tau(a_{ij},a_{j}))$$ $$\tau(a_{i},a_{ij}) = (a_{i} \rightarrow a_{ij}, a_{ij} \dashrightarrow a_{i})_{\circlearrowleft}$$ $$\tau(a_{ij},a_{j}) = (a_{ij} \rightarrow a_{j}, a_{j} \dashrightarrow a_{ij})_{\circlearrowleft}$$

其中 $\tau(\cdot)$ 代表智能体之间的交互，$\rightarrow$ 表示请求的行为，$;$（即公式中的分号或对应符号）表示相应的回复——在此过程中批评者提供指令（Instruction），行动者提供产物（Artifact），而 $\circlearrowleft$ 表示一个迭代过程 1。

也就是说，$a_{i}$ 请求反馈，$a_{ij}$ 提供经过反思的建议并请求进一步精炼，而 $a_{j}$ 提供精炼后的产物 2。因此，与单条边相关联的智能体可以进行迭代式的反思与精炼，从而有效地实现对前一个产物的优化 3。 Figure 4

Memory Control

值得注意的是，智能体之间无限制的信息交换不可避免地导致上下文爆炸，最终通过限制对额外实体的支持来阻碍可扩展性。为了解决这个问题，作者采用短期和长期记忆来管理每个智能体的上下文可见性。短期记忆捕捉每次交互中的工作记忆，确保上下文感知的决策制定。长期记忆通过仅保留源自当前对话的最终产物，而不是整个对话历史，来保持上下文的连续性，从而确保非产物上下文（例如产物之前的详细分析过程）对后续智能体保持不可访问。该机制确保只有产物在网络中传播，这在保持连续性的同时，显式地最小化了上下文爆炸的风险。产物通过在发散节点处分支，或在需要有效聚合的收敛节点处合并来进行传播；从技术上讲，在精炼之前，收敛智能体通过层次化聚合整合传入产物的优势，从而产生一个“非线性”强度聚合的产物。

理论上，在以最高交互密度为特征的网状（mesh）结构中，对于承受最大上下文压力的汇聚智能体（sink agent），在没有和有该机制（记忆控制）的情况下的总 Token 消耗推导如下：

$$\mathcal{O}(n)_{w/o} = t + p + s + (2m - 1)(i + s)(n(n - 1)/2 + 2(n - 2)) \stackrel{n\gg1}{\approx} Cn^2 \propto n^2$$ $$\mathcal{O}(n)_{w/} = t + p + s + m(i + s)((n - 1) + 2(n - 2)) \stackrel{n\gg1}{\approx} \bar{C}n \propto n$$

其中

$$C \equiv (2m - 1)(i + s)/2$$ $$\bar{C} \equiv 3m(i + s)$$

这里 $n$ 是网络规模（即 $|\mathcal{V}|$），$t$ 是任务长度，$p$ 是角色设定（profile）长度，$i$ 是平均指令长度，$s$ 是平均产物长度，而 $m$ 是相邻智能体之间的最大交互轮数。

这种 Token 复杂度分析表明，如果没有记忆控制，上下文长度将随 $n^2$ 增长，导致随着网络规模的扩大，时间和成本呈平方级增加。相反，作者的机制将上下文长度的增长从二次方解耦为线性增长，从而有效地抑制了上下文爆炸，并使更大规模的网络具备了更好的可扩展性。

评估（Evaluation）

Baselines

  • Cot
  • AutoGPT
  • GPTSwarm
  • AgentVerse

Datasets & Metrics

  • MMLU: 逻辑推理问题
  • HumanEval: 代码生成问题
  • SRDD: 仓库级代码生成问题
  • CommonGen-Hard: 写作能力

性能

Table 1 作者采用链式拓扑结构作为比较分析的默认设置，链式拓扑结构已经基本上优于所有baseline了。与单一智能体相比，MACNET-Chain主要优势在于促进了一种过程式思维，在此过程，产物被不断反思和精炼，这一过程可以有效缓解幻觉。CoT在某些数据集上已经表现出强劲的性能了，这主要是因为广泛研究的基准测试的底层只是已经嵌入在基础模型中，使得单智能体在这些相对“简单”的任务中具备显著能力。虽然GPTSWARM通过节点和边的动态优化来对智能体进行自组织，但它需要针对所有节点和边进行大量的特定任务定制，这增加了使用的复杂性，从而阻碍了其向异构下游任务的无缝泛化。鉴于对高性能和自动化现实世界系统的需求日益增长，期望所有预备知识都能完全预编码在基础模型中，或者为所有不可预见的复杂任务预先制定特定的适配方案，都是不切实际的。MACNET通过简单的超参数（如拓扑类型和规模）自动生成各种网络来弥合这一差距，使智能体能够在无需特定调整的情况下进行协作交互，这代表了实现自主性和泛化性的一条有希望的途径。此外，作者通过去除智能体的角色设定（Profile）来模拟退化为使用简化智能体的思维图（Graph-of-Thought）推理（Besta et al., 2024a），这导致所有拓扑结构的平均性能下降了3.67%。这一结果突显了群体智能（collective intelligence）相对于单一视角推理的有效性，因为后者代表了多智能体环境中一种形式的降维，不可避免地阻碍了其探索潜在机会的潜力。

不同的拓扑性能比较

稠密度 上表展示了不同类型的拓扑结构在特定任务上的有效性存在显著差异；没有一种单一的拓扑结构能在所有任务中始终表现出色。例如，链式（chain）拓扑更适合软件开发，而树状（tree）拓扑则是创意写作的理想选择。这种现象可能源于软件工程本质上适合线性流程，该流程通过分析、编码、审查和测试等顺序步骤来完成；相比之下，需要高创造力的任务需要更发散的结构，以促进智能体从不同切面（aspects）进行交互。此外，与边密度（edge density） 相关的更高交互密度（见下图），与三种主要拓扑类型的平均性能提升呈正相关。具体而言，连接紧密的网状（mesh） 拓扑优于中等密度的树状拓扑，而后者又优于连接稀疏的链式拓扑。

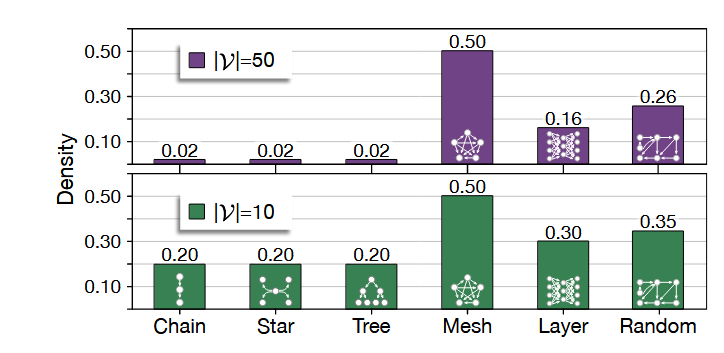
Figure 5

形状 尽管最密集的交互（即网状结构）在直观上很吸引人，但它们并不总能带来最佳的性能。相反，不规则拓扑结构通常表现出统计学上显著的优势。作者猜测这一现象是因为过密的交互会让智能体陷入信息过载，从而阻碍了有效的反思和精炼。相反，网络随机化经常引发小世界属性（Small-world properties）（Watts & Strogatz, 1998），其特征是更短的平均路径长度或更高的聚类系数。这些随机的边连接就像残差连接（Residual Connections）一样，可以通过直接捷径（Shortcuts）连接“不相识”的智能体，把它们变成“熟人”，隐式地减少了平均路径长度，这自然降低了长距离产物不可见的可能性。这种现象与现实世界中成熟的规则组织结构相比似乎有些反直觉，它表明智能体世界中的协作模式不必完全复刻人类社会的模式。此外，随机拓扑结构比网状拓扑结构节省约 51.92% 的时间，在降低密度和提高效率之间取得了最佳平衡，因此成为一种更实际的选择。作者还注意到，在相同密度下，“更宽”的星形拓扑结构往往比“更深”的树形拓扑结构表现更好。这主要是由于记忆控制机制造成的；虽然它有效地管理了过长上下文在网络中的传播，但也可能导致深层拓扑结构失去对远端智能体的追踪，偶尔导致产物版本回滚（Qian et al., 2024a）。这也指向了一种经验性的搜索策略，即通过自动搜索或人工设计来管理网络规模和聚类系数，以在有效性和效率之间找到最佳平衡。

深入研究后，一项深度的归纳偏置分析表明，在封闭域场景（例如逻辑选择）中，链式结构显著有助于促进循序渐进的推理。相反，并行的分支（例如星形）增多可能导致令人费解的头脑风暴，这并不总是有利的。在开放域场景中，以更多收敛节点（Convergent nodes）为特征的拓扑结构显示出能更频繁地修改产物并产生更长的产物。这是因为更多的收敛节点带来了更高的输入多样性，增加了精炼产物的可能性，从而有利于长度敏感的指标，因为更长的产物更有可能满足丰富的需求。最终，没有任务是局限于特定拓扑结构的；最佳配置应根据场景的开放性、可用的计算资源以及相关的推理成本来选择。

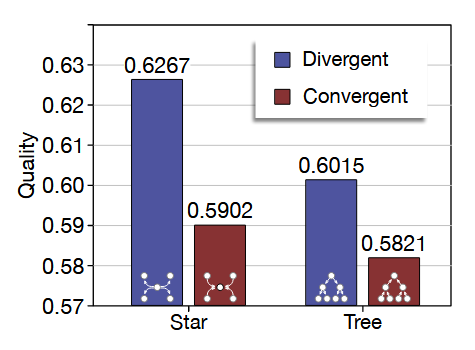
方向 除了密度和形状的视角之外，某些拓扑结构中内在的不对称性——即反转边会导致拓扑上截然不同的配置——引起了作者的兴趣，促使作者探索反向拓扑的影响。如下图所示，仅仅反转特定拓扑结构的方向就可能导致显著的性能下降。通常，以拥有比父节点更多的子节点为特征的发散型（divergent）拓扑，其表现大幅优于其收敛型（convergent）对应结构。直观地说，产物（artifact）的传播发散过程是平滑的，使得每个智能体能够从不同的切面（aspects）讨论产物。相比之下，在收敛节点处聚合多个产物更具挑战性，这突显了将多样化的切面整合到一个连贯产物（cohesive artifact）中的复杂性。因此，为了最小化产物聚合过程中的潜在退化，建议采用那些最大化发散同时最小化收敛的拓扑结构。

Figure 6

是否遵守拓展法则

Figure 7

趋势 回顾神经缩放定律（neural scaling law），它假设增加神经元会导致性能的持续提升。为了探究协作缩放定律（collaborative scaling law）——旨在挖掘智能体规模与性能之间的关系——作者尝试将节点数量（$|V|$）从 $2^0$（退化为单智能体变体）指数级增加到 $2^6$（相当于网状网络中的一千多个智能体）。如上图所示，扩展作者的网络最初在各种多智能体系统生成的产物质量上增长缓慢，随后带来快速的提升，最后达到一个饱和点。这种模式类似于一个 Sigmoid 变体函数：

$$f (|V|) = \frac{\gamma}{1 + e^{-\beta(\log |V|-\alpha)}} + \delta \quad (6)$$

其中 $\{\alpha, \beta, \gamma, \delta\}$ 是针对特定拓扑结构的实数参数。粗略地说，$2^4$（即 16 个）左右的节点数量似乎是一个合理的选择。然而，考虑到稀疏拓扑的效率和密集拓扑的优越性能，作者提倡在将这一趋势应用于各种下游应用时，通过多维权衡来平衡形状和规模。这一发现表明，许多现有的智能体系统可能未发挥出全部潜力，这强调了一条通过增加智能体数量来提升性能的有希望的路径（前提是它们能有效协作），而不仅仅是专注于扩展基础模型。

此外，对基线扩展的验证表明，平衡LLM调用次数——无论是在封闭域任务中通过多数投票（Majority Voting），还是在开放域任务中通过Best-of-N——始终突显了所有基线都缺乏有效的可扩展性。即使在结合CoT或 AutoGPT时，多数投票仅将性能提升了 0.9%，并且在大约8个智能体时进入瓶颈期。AgentVerse隐式地退化为星形拓扑，并且在扩展超过30个智能体时经常遇到上下文爆炸问题，从而阻碍了可扩展性。GPTSwarm的高能耗设置需要人工的、特定于任务的结构化和提示工程，这限制了多任务处理能力和整体可扩展性。

时序 神经缩放定律（Neural Scaling Law）需要模型拥有至少十亿参数和超过 $10^{22}$ 次训练 FLOPs 才能显示出涌现趋势。相比之下，MACNET 中的协作涌现（Collaborative Emergence）在小得多的规模上就会显现，大多数拓扑结构在大约一百个智能体时即达到性能饱和。根本原因是，神经元协调（在训练期间）依赖于数值矩阵运算，需要所有神经元从头开始精确且同时地学习，以吸收广泛的世界知识。相反，个体智能体（在推理期间）已经从基础模型中拥有了某些知识，它们通过相互依赖的交互进行的协调利用了现有的推理技能来传播来自不同切面的知识；智能体交互中用于产物精炼的最关键切面通常不需要如此大的规模就能被充分反思和精炼。因此，除了神经元协作之外，智能体协作可以作为提升智能水平的一条捷径，特别是当数据和硬件等大规模重训资源受限时。

什么因素有助于多智能体协作

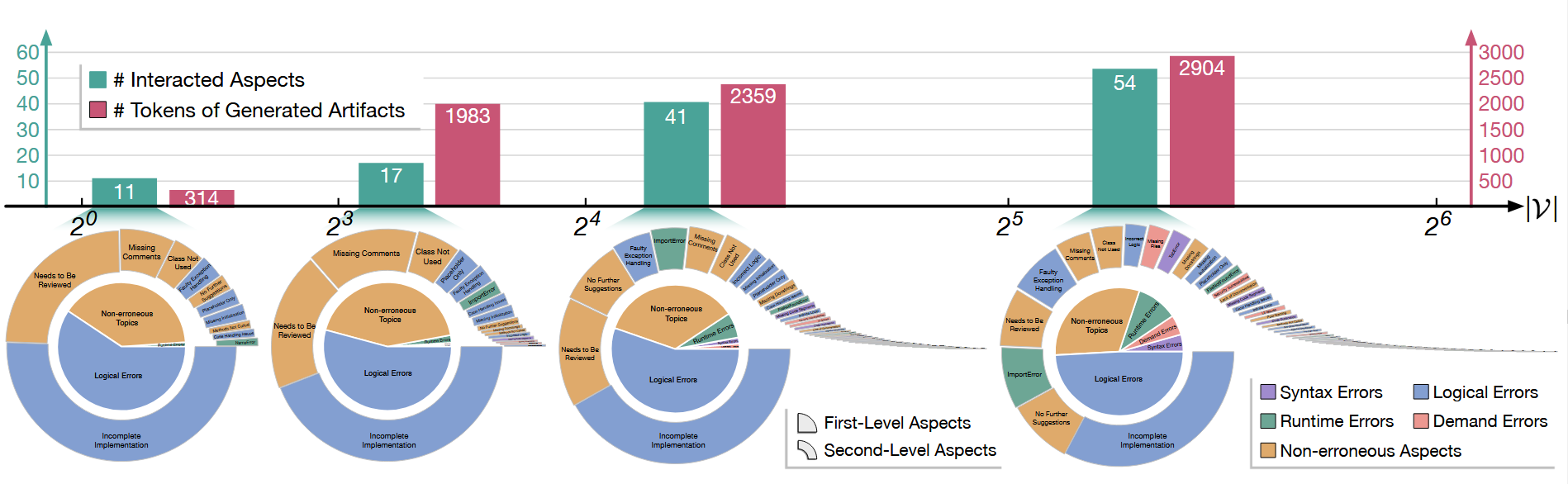
Figure 8

为了深入探究其潜在机制，作者选择了软件开发中使用的中等密度的分层（layer）拓扑作为代表性案例，类似的现象在其他拓扑结构和场景中也一贯存在。具体来说，作者将智能体交互中讨论的切面分为五大类：四个层级的错误（语法、运行时、逻辑和未满足的需求）以及一个非错误类别；每个类别包含多个子类别。上图展示了交互切面的总数及其详细分布。在较小的拓扑结构（$2^0 \le |V| \le 2^3$）中，有限的交互密度将切面限制在大约十几个次级切面。然而，随着网络扩展（$2^4 \le |V| \le 2^6$），交互密度呈二次方增加，导致切面数量突然增加到几十个，随后的增长更为平缓。这一进展与观察到的涌现能力趋势紧密平行，这可能将涌现部分归因于智能体之间详细交互切面的急剧增加。这种现象的发生是因为底层模型的 Token 分布通常遵循长尾模式（long-tail pattern），需要更大规模的采样才能可能捕获这些尾部 Token。因此，这鼓励了更多罕见的“尾部切面”的涌现，使得协作过程能够扩展到最常见的切面之外。理论上，长尾 Token $t$ 在 $n$ 次采样中至少出现一次的概率为：

$$p_{n}(t) = 1 - (1 - p(t))^{n} \propto 1 - (1 - 1/r(t))^{|V|^{2}}$$ $$\lim_{|V| \to \infty} p_{n}(t) = \lim_{n \to \infty} p_{n}(t) = 1 \quad (7)$$

其中 $p(t) \propto 1/r(t)$ 代表描述长尾分布的标准齐普夫定律（Zipf’s law）；样本大小 $n$ 与交互密度成正比，即 $n \propto |V|^2$。可以推断，增加网络规模会显著提高尾部 Token 出现的概率，并逐渐接近渐近线。一旦样本量足够大，这种概率就会变成必然事件。据统计，当批评者提出特定的切面建议时，行动者有 93.10% 的统计可能性会实施建议的精炼，而不是忽略它。规模的扩大使得批评者能够查明产物中更细微的问题，引导行动者启动相应的精炼。因此，协作过程中的每一轮对话都从不同的切面精炼产物，自然提高了产生更细致入微产物的概率。

针对多维度的考虑，相应地扩展智能体规模会延长产物的总长度。例如，当规模从 $2^0$ 增加到 $2^4$ 时，Token 长度增加了7.51倍。这种特性在小规模网络上促进了对详细需求、性能优化以及其他高级因素的整合，可能涵盖了短产物无法包含的能力。这主要是由于图本身自然的发散和收敛拓扑结构，使得产物能够进行强度聚合的精炼（strength-aggregated refinement）传播。因此，与多数投票（Majority Voting）不同，这种范式促进了多样化产物之间相互依赖的交互和长度扩展的再生，从而产生更全面的产物。

优点与创新点 (Strengths)

  • 验证了智能体的缩放定律，理论上通过Zipf’s Law和长尾分布理论来进行解释。

我的思考

在多智能体项目中可以尝试使用智能体对话形式进行产物优化。